La teoría de juegos es un marco teórico para concebir situaciones sociales entre jugadores que compiten entre sí. En algunos aspectos, la teoría de juegos es la ciencia de la estrategia, o al menos de la toma de decisiones óptimas de actores independientes y competidores en un entorno estratégico. Veamos algunos ejemplos.
Los principales pioneros de la Teoría de Juegos fueron el matemático John von Neumann y el economista Oskar Morgenstern en la década de 1940. El matemático John Nash es considerado por muchos como la primera extensión significativa del trabajo de von Neumann y Morgenstern.
Traducido y adaptado del original "Introduction to Game Theory", por Trishna Patnaik en el blog de Innovation Management
LOS FUNDAMENTOS DE LA TEORÍA DE JUEGOS
El centro de la teoría de juegos es el juego, que sirve como modelo de una situación interactiva entre jugadores racionales. La clave de la teoría de juegos es que la retribución de un jugador depende de la estrategia aplicada por el otro. El juego identifica las identidades de los jugadores, sus preferencias y las estrategias disponibles y cómo estas estrategias afectan al resultado. Dependiendo del modelo, pueden ser necesarios otros requisitos o supuestos.
La teoría de juegos tiene una amplia gama de aplicaciones, como la psicología, la biología evolutiva, la guerra, la política, la economía y los negocios. A pesar de sus muchos avances, la teoría de juegos se considera todavía una ciencia joven y en desarrollo. Según la teoría de juegos, las acciones y elecciones de todos los participantes afectan al resultado de cada uno.
EMPECEMOS POR EL EQUILIBRIO DE NASH
El Equilibrio de Nash es un resultado alcanzado que, una vez conseguido, significa que ningún jugador puede aumentar la ganancia cambiando las decisiones unilateralmente. También puede considerarse como "sin arrepentimiento", en el sentido de que una vez tomada una decisión, el jugador no se arrepentirá de sus decisiones teniendo en cuenta las consecuencias que conllevan.
El equilibrio de Nash se alcanza con el tiempo, en la mayoría de los casos. Sin embargo, una vez alcanzado el Equilibrio de Nash, no se desviará de él. Después de aprender a encontrar el Equilibrio de Nash, mira cómo afectaría un movimiento unilateral a la situación. ¿Tiene algún sentido? No debería, y por eso el Equilibrio de Nash se describe como "sin remordimientos". En general, se considera que existe más de un equilibrio en un juego.
Esto ocurre principalmente en juegos con elementos más complejos que con dos elecciones de dos jugadores. En los juegos simultáneos que se repiten a lo largo del tiempo, uno de estos equilibrios múltiples se alcanza después de algún ensayo y error. Este mismo escenario de diferentes elecciones a lo largo del tiempo antes de alcanzar el equilibrio se da con mayor frecuencia en el mundo de los negocios cuando dos empresas determinan los precios de productos altamente intercambiables, como las tarifas aéreas o incluso los refrescos.
IMPACTO DE LA TEORÍA DE JUEGOS EN LA ECONOMÍA Y EN LA EMPRESA
La teoría de los juegos ha supuesto una revolución en la economía al resolver problemas cruciales de los modelos económicos matemáticos anteriores. Por ejemplo, la economía neoclásica tenía dificultades para entender la anticipación empresarial y no podía manejar la competencia imperfecta. La teoría de los juegos desvió la atención del equilibrio estacionario hacia el propio proceso de mercado.
En el ámbito empresarial, la teoría de los juegos es definitivamente beneficiosa para modelar los comportamientos competitivos entre los agentes económicos. Las empresas suelen tener varias opciones estratégicas que afectan a su capacidad de obtener beneficios económicos. Por ejemplo, las empresas pueden enfrentarse a dilemas como el de retirar los productos existentes o empezar a desarrollar otros nuevos, bajar los precios con respecto a la competencia o emplear nuevas estrategias de marketing. Los economistas suelen utilizar la teoría de los juegos para entender el comportamiento de las empresas en oligopolio. Ayuda a predecir los resultados probables cuando las empresas adoptan determinados comportamientos, como la fijación de precios y la colusión.
TIPOS DE TEORÍA DE JUEGOS
Aunque hay muchos tipos (por ejemplo, simétrica/asimétrica, simultánea/secuencial, etc.) de teorías de juegos, las teorías de juegos cooperativos y no cooperativos son las más comunes. La teoría de los juegos cooperativos trata de cómo interactúan las coaliciones, o los grupos cooperativos, cuando sólo se conocen las compensaciones. Se trata de un juego entre coaliciones de jugadores y no entre individuos, y cuestiona cómo se forman los grupos y cómo reparten los beneficios entre los jugadores.
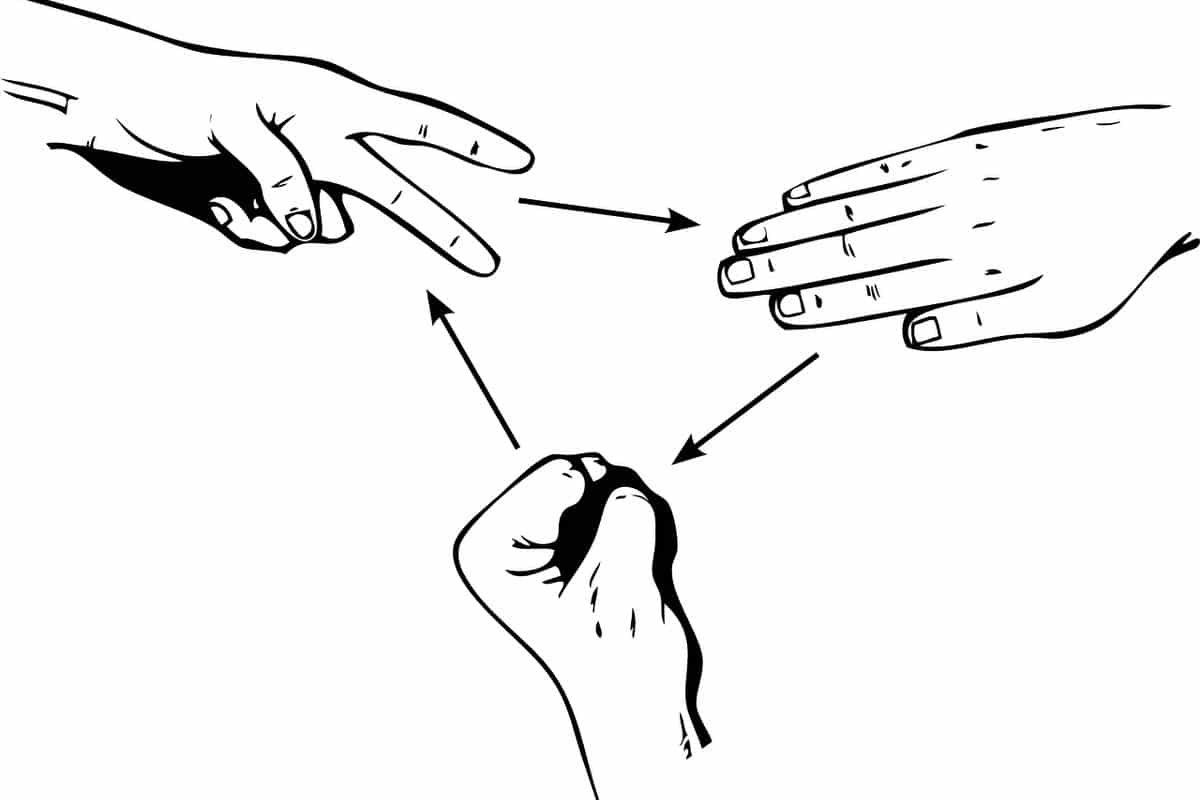
La teoría de los juegos no cooperativos se ocupa de cómo los agentes económicos racionales tratan entre sí para alcanzar sus propios objetivos. El juego no cooperativo más común resulta ser el juego estratégico, en el que sólo se enumeran las estrategias disponibles y los resultados que se derivan de una combinación de elecciones. Un ejemplo simplista de juego no cooperativo en el mundo real es Piedra-Papel-Tijeras.
Ejemplos de la teoría de los juegos: Hay varios "juegos" que analiza la teoría de juegos.
A continuación, describiremos brevemente algunos de ellos.
El dilema del prisionero
El dilema del prisionero es el ejemplo más conocido de la teoría de juegos. Consideremos el ejemplo de dos delincuentes detenidos por un delito. Los fiscales no tienen pruebas sólidas para condenarlos. Sin embargo, para obtener una confesión, los funcionarios sacan a los presos de sus celdas de aislamiento y los interrogan a cada uno en cámaras separadas. Ninguno de los presos tiene medios para comunicarse entre sí. Los funcionarios presentan cuatro tratos, a menudo expuestos como una caja de 2 x 2.
-Si ambos confiesan, cada uno recibirá una condena de cinco años de prisión.
-Si el prisionero 1 confiesa, pero el prisionero 2 no, el prisionero 1 recibirá tres años y el prisionero 2 nueve años.
-Si el prisionero 2 confiesa, pero el prisionero 1 no lo hace, el prisionero 1 recibirá 10 años y el prisionero 2 dos años.
-Si ninguno de los dos confiesa, cada uno cumplirá dos años de prisión.
La estrategia más favorable es entonces no confesar. Sin embargo, ninguno de los dos conoce la estrategia del otro y, sin la certeza de que uno de ellos no confesará, es probable que ambos confiesen y reciban una condena de cinco años de prisión. El equilibrio de Nash sugiere que en un dilema del prisionero, ambos jugadores harán la jugada que sea mejor para ellos individualmente pero peor para ellos colectivamente.
Se ha determinado que la expresión "ojo por ojo" es la estrategia óptima para optimizar el dilema del prisionero. El "ojo por ojo" fue introducido por Anatol Rapoport, que desarrolló una estrategia en la que cada participante en un dilema del prisionero iterado sigue un curso de acción consistente con el turno anterior de su oponente. Por ejemplo, si es provocado, un jugador responde posteriormente con represalias; si no es provocado, el jugador coopera.
Juego del dictador
Se trata de un juego sencillo en el que el jugador A debe decidir cómo repartir un premio en metálico con el jugador B, que no tiene nada que ver con la decisión del jugador A. Aunque no se trata de una estrategia de teoría de juegos propiamente dicha, sí que proporciona algunas ideas interesantes sobre el comportamiento de las personas. Los experimentos revelan que aproximadamente el 50% se queda con todo el dinero, el 5% lo reparte a partes iguales y el otro 45% da al otro participante una parte menor.
El juego del dictador está muy relacionado con el juego del ultimátum, en el que el jugador A recibe una cantidad de dinero determinada, parte de la cual tiene que entregar al jugador B, que puede aceptar o rechazar la cantidad entregada. El problema es que si el segundo jugador rechaza la cantidad ofrecida, tanto A como B no reciben nada. Los juegos del dictador y del ultimátum ofrecen importantes lecciones para cuestiones relacionadas con causas como la caridad y la filantropía.
Dilema del voluntario
En el dilema del voluntario, alguien tiene que realizar una tarea o un trabajo por el bien común. El peor resultado posible se produce si nadie se ofrece como voluntario. Por ejemplo, pensemos en una empresa en la que el fraude contable es galopante, aunque la alta dirección no es consciente de ello. Algunos empleados subalternos del departamento de contabilidad están al tanto del fraude, pero dudan en decírselo a la alta dirección porque eso supondría el despido de los empleados implicados en el fraude y, muy probablemente, su procesamiento judicial.
Ser calificado de denunciante también puede tener algunas repercusiones y consecuencias en el futuro. Pero si nadie se ofrece como voluntario, el fraude a gran escala puede provocar la quiebra de la empresa y la pérdida de los puestos de trabajo de todos.
El juego del ciempiés
El juego del ciempiés es un juego de forma extensiva en la teoría de juegos en el que dos jugadores tienen alternativamente la oportunidad de llevarse la mayor parte de un depósito de dinero que aumenta lentamente. Está organizado de tal manera que si un jugador pasa el incremento a su oponente, que se lo lleva, el jugador recibe una cantidad menor que si se hubiera llevado el bote.
El juego del ciempiés concluye en cuanto un jugador se lleva el bote, y ese jugador se lleva la parte más grande y el otro la más pequeña. El juego tiene un número total predefinido de rondas, que cada jugador conoce con bastante antelación.
LIMITACIONES DE LA TEORÍA DE JUEGOS
El mayor problema de la teoría de los juegos es que, al igual que la mayoría de los modelos económicos, se basa en el supuesto de que las personas son actores racionales que tienen un interés propio y maximizan la utilidad. Somos seres sociales que cooperamos y nos preocupamos por el bienestar de los demás, a menudo a costa nuestra. La teoría de los juegos no puede dar cuenta de que en algunas situaciones podemos caer en el equilibrio de Nash y en otras no, dependiendo del contexto social y de quiénes sean los jugadores.
JUEGOS REPETIDOS DE OLIGOPOLIO
El dilema del prisionero se jugó una vez, por dos jugadores. Los jugadores recibían una matriz de pagos; cada uno podía hacer una elección, y el juego terminaba después de la primera ronda de elecciones.
En el mundo real del oligopolio hay tantos jugadores como empresas en el sector principal. Juegan ronda tras ronda: una empresa sube su precio; otra empresa introduce un nuevo producto, cuando la primera empresa baja su precio, entonces una tercera empresa introduce una nueva estrategia de marketing, y así sucesivamente. Un juego de oligopolio es un poco como un partido de béisbol con un número ilimitado de entradas: una empresa puede salir ganando después de una ronda, y otra saldrá ganando otro día. Por ejemplo: En el juego de la industria informática, la introducción de los ordenadores personales cambió las reglas. IBM, que había ganado el juego de los ordenadores centrales con bastante facilidad, lucha por mantener el ritmo en un mundo en el que los rivales siguen rebajando los precios y mejorando la calidad.
Los juegos de oligopolio pueden tener más de dos jugadores, por lo que las partidas son mucho más complejas, pero esto no cambia su estructura básica. El hecho de que los mismos juegos se repitan introduce nuevas consideraciones estratégicas. Un jugador debe tener en cuenta no las formas en que sus elecciones afectarán a sus rivales, sino cómo sus elecciones les afectarán a ellos también en el futuro.
Mantengamos el juego simple ahora, y consideremos un juego de duopolio. Las dos empresas se han confabulado, tácita o abiertamente, para crear una solución de monopolio. Mientras cada jugador mantenga el mismo acuerdo, las dos empresas obtendrán el máximo beneficio económico posible en la misma empresa.
PROCESO DE TOMA DE DECISIONES
La teoría de los juegos se ocupa de la toma de decisiones en un mundo interactivo en el que la mejor decisión de cada responsable depende de las decisiones que tomen los demás. Por tanto, en este mundo interactivo, cada uno, para avanzar en su propio interés, tendrá que predecir las decisiones de los demás.
La teoría de los juegos entró oficialmente en el mundo en el año 1944 con la publicación de la obra magna de la teoría de los juegos, "Theory of Games and Economic Behavior". Fue una colaboración conjunta entre el economista austriaco Oskar Morgenstern y John von Neumann, un genio, polímata y políglota húngaro universalmente aclamado.
Von Neumann era un genio indiscutible, pero era un mediocre jugador de póquer y pronto se dio cuenta de que la teoría de la probabilidad no puede ayudar a ganar partidas de póquer. Su gran aprecio por la información imprecisa, las dudas y la imprevisibilidad de las partidas de póquer sentó las bases de la teoría del juego: cómo los jugadores de póquer pueden ocultar información liberando estratégicamente información a través de sus jugadas y provocando los errores de los rivales.
En otras palabras, formalizó cómo los jugadores de póquer pueden "farolear" a sus rivales jugando con una serie de estrategias que se supone que engañan a sus rivales y ocultan información para finalmente ganar la partida.
El legado de John Nash en la teoría de los juegos es un equilibrio de Nash único y alcanzable, y la teoría de los juegos se convirtió así en algo totalmente clínico y totalmente alejado del mundo real. Las únicas excepciones entre los economistas consumados de hoy son otros dos premios Nobel, Thomas C. Schelling y Roger Myerson.
SI TODOS FUÉRAMOS MEJORES PERSONAS, EL MUNDO SERÍA UN LUGAR MEJOR
Parte del poder y el significado de la teoría de juegos puede ilustrarse evaluando la afirmación "Si todos fuéramos mejores personas, el mundo sería un lugar mejor". Esto puede parecerle una verdad evidente. O incluso puede reconocer que, como cuestión de lógica, esto implica la falacia de la composición: el hecho de que una afirmación se aplique a una persona individual no tiene por qué aplicarse a todo el grupo.
La teoría de los juegos puede dar un sentido preciso a la afirmación tanto de lo que significa ser un pueblo mejor como de lo que significa que el mundo sea un lugar mejor, y por tanto permite demostrar o refutar la misma afirmación. De hecho, la afirmación es falsa, y esto puede demostrarse mediante una variación del dilema del prisionero.
¿QUÉ CONCLUSIONES PODEMOS SACAR?
La clave de la teoría de los juegos y para entender por qué las personas mejores pueden hacer del mundo un lugar peor es comprender el delicado equilibrio. Es cierto que si simplemente nos volvemos más solidarios y no ocurre nada más, el mundo al menos no será peor. Sin embargo: la paradoja inicia que si nos volvemos más solidarios desearemos cambiar cómo nos comportamos particularmente. Así que cuando intentamos hacerlo al mismo tiempo, el resultado final puede ser que todos estemos peor. ¡Así que eso es lo que ejemplifica y contradice la Teoría del Juego al mismo tiempo!
AUTORA
Trishna Patnaik, licenciada en Ciencias de la Vida y con un MBA en Marketing, es artista por elección propia. Artista autodidacta afincada en Mumbai, Trishna lleva más de 14 años practicando el arte. Después de trabajar en varias empresas de renombre, se dio cuenta de que quería hacer algo más significativo. Encontró su verdadera vocación en su pasión, la pintura. Trishna es ahora una pintora profesional a tiempo completo que persigue su pasión por crear y explorar al máximo. Dice: "Es un camino menos transitado, pero un viaje que me hace ilusión cada día". Trishna también imparte talleres de pintura en Mumbai y otras ciudades metropolitanas de la India.
Trishna es terapeuta de arte y sanadora. Trabaja con clientes de forma individual en Bombay. A Trishna le gusta el arte de la escritura creativa y está metiendo las manos en eso también, para empaparse de la experiencia y tener un compromiso con los lectores, viajeros y pensadores.
IMAGEN: la del artículo original